Question

You select a random sample of n=14 families in your neighborhood and find the following family sizes (number of people in the family)

10,11,14,13,12,10,11,11,10,11,10,11,12,13

An estimate for the mean family size for the population is__

(round to the nearest tenth as needed)

What is the 95% confidence interval for the estimate?

__
(round to the nearest tenth as needed)

Comment on the reliability of the estimate. Choose the correct answer below.

The sample is unlikely to be very representative of all families in a country.

The sample is unlikely to be representative of all families in a country.

There is not enough data to make a conclusion.

Answer 1

a) An estimate for the mean family size for the population is 11.357

b) The 95% confidence interval is given by (10.6;12.1)

c) The sample is unlikely to be very representative of all families in a country.

The reason whyis because the random sample is not higher and in order to increase the accuracy of the results we need to take a larger sample size to be sure about the conclusions.

Explanation:

Previous concepts

The margin of error is the range of values below and above the sample statistic in a confidence interval.

Normal distribution, is a "probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean".

Solution to the problem

Assuming the X follows a normal distribution

`X \sim N(\mu, \sigma)`

The distribution for the sample mean is given by:

`\bar X \sim N(\mu, (\sigma)/(√(n)))`

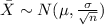
Data given: 10,11,14,13,12,10,11,11,10,11,10,11,12,13

Part a

We can calculate the sample mean and deviation with the following formulas:

`\bar X = (\sum_(i=1)^n X_i)/(n)`

`s=\sqrt{(\sum_(i=1)^n (X_i -\bar X)^2)/(n-1)}`

`\bar x =11.357` represent the mean

An estimate for the mean family size for the population is 11.357

`s=1.277` represent the sample standard deviation

n= 14 sample size selected.

Part b

The confidence interval is given by this formula:

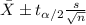`\bar X \pm t_(\alpha/2) (s)/(√(n))` (1)

And for a 95% of confidence the significance is given by
`\alpha=1-0.95=0.05`, and
`(\alpha)/(2)=0.025`.

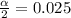We need to calculate the degrees of freedom first like this:

`df= n-1= 14-1 =13`

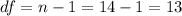
Since we don't know the population standard deviation we can calculate the critical value
`t_(0.025)= \pm 2.16`

`n=14,\bar X=11.357,s=1.277`

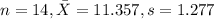
If we use the formula (1) and we replace the values we got:

`11.357 - 2.16 (1.277)/(√(14))=10.620`

`11.357 + 2.16 (1.277)/(√(14))=12.094`

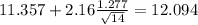
The 95% confidence interval is given by (10.6;12.1)

Part c

The sample is unlikely to be very representative of all families in a country.

The reason whyis because the random sample is not higher and in order to increase the accuracy of the results we need to take a larger sample size to be sure about the conclusions.