Answer:
a)
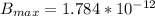
Step-by-step explanation:
Given paraeters are:
R = 25 cm
d = 4.7 mm
f = 60 Hz
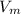 = 160 V
= 160 V
a)
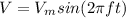
Where
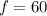 Hz and
Hz and
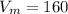 V
V
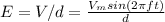
For
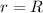

Since
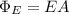
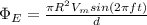
From Ampere's Law:
 where
where
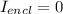
So at
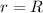 ,
,
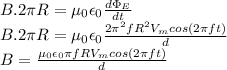
For maximum B, cos(2πft) = 1. Hence,
 T
T
b) From r = 0 to r = R = 0.025 m, by Ampere's Law, the equation will be:
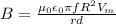
From r = R = 0.025 m to r = 0.1 m, by Ampere's Law, the equation will be:
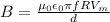
The plot is given in the attachment.