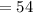Question

Evaluate 10m +\dfrac {n^2}410m+ 4 n 2 ​ 10, m, plus, start fraction, n, squared, divided by, 4, end fraction when m=5m=5m, equals, 5 and n=4n=4n, equals, 4.

Answer 1

Answer:
`54`

Explanation:

Given the following expresion provided in the exercise:

`10m+(n^2)/(4)`

You can follow these steps in order to evaluate it when
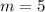`m=5` and
`n=4`:

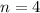1. You need to substitute
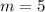`m=5` and
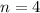`n=4` into the given expression:

`10(5)+((4)^2)/(4)`

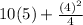
2. Now you can solve the mutiplication:

`=50+((4)^2)/(4)`

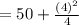
3. Since
`4^2=4*4`, you get:

`=50+(16)/(4)`

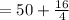
4. You must solve the division. Divide the numerator 16 by the denominator 4. Then:

`=50+4`

5. And finally, you must solve the addition. So, you get this result:

`=54`