Answer:
The Blue Marble should be worth 8 points for the game to be fair
Explanation:
Discrete Distribution
It refers to the situation where a finite and known number of outcomes are equally likely to happen, like the throw of the die where each side has 1/6 probability to be shown.
Marlene has five different colored marbles, each one with the same probability of occurrence of 1/5. Each time a color other than blue is chosen the player loses 2 points. Let's call X the number of points a player receives if a blue marble is chosen.
The expected value of this distribution is

Where
 are the earnings of each possible chosen marble and
are the earnings of each possible chosen marble and
 are the probability to choose each marble, they are all the same. So
are the probability to choose each marble, they are all the same. So


To be fair (no win, no lose), E should be zero

So
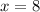
This means that when we choose the blue marble, we should get 8 points to get a fair bet