Answer:
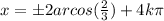
where
 is an integer
is an integer
Explanation:

We are going to isolate the trig expression first.
Subtract 5 on both sides:

Divide both sides by 3:

Now since
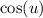 is even then
is even then
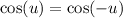 .
.
So we have:

implies:
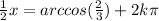
Multiply both sides by 2:
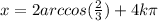
or
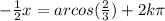
Multiply both sides by -2:
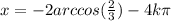
So we can say the solution is:

(
 is an integer)
is an integer)