Question

Mercedes bought some vanilla cupcakes and some chocolate cupcakes. If she

eats one of the vanilla cupcakes, then of the remaining cupcakes will be
vanilla. If Mercedes instead eats two of the chocolate cupcakes, then = of the
remaining cupcakes will be vanilla. How many cupcakes did Mercedes buy?

Answer 1

we need numbers to answer the question

Explanation:

Answer 2

Here is the full question

Mercedes bought some vanilla cupcakes and some chocolate cupcakes. If she eats one of the vanilla cupcakes, then 1/7 of the remaining cupcakes will be vanilla. If Mercedes instead eats two of the chocolate cupcakes, then 1/5 of the remaining cupcakes will be vanilla. How many cupcakes did Mercedes buy?

Answer:

22

Explanation:

Let represent the number of vanilla cupcakes=v

and the number of chocolate cupcakes=c

So, total number of cupcakes Mercedes bought = (v+c)

When she eats 1 vanilla cupcake

Number of vanilla cupcakes remaining=v-1

Number of cupcakes remaining=v+c-1

However;

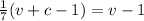`(1)/(7)(v+c-1) = v- 1` -------------------- equation 1

If Mercedes instead eats two of the chocolate cupcakes

Number of chocolate cupcakes remaining=c-2

However

`(1)/(5)(v+c-2) = v` --------------------- equation 2

From equation (1)

`(1)/(7)(v+c-1) = v- 1`

`v+c-1 = 7(v-1)`

`v+c -1 = 7v -7`

`c-1+7 = 7v -v`

`c+6 = 6v`

`6 = 6v - c`

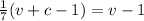
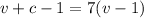
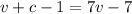
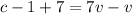
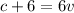
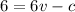
`6v-c = 6` --------------------- equation (3)

From equation(2)

`(1)/(5)(v+c-2) = v`

`v+c-2 =5v`

`c-2 = 5v-v`

`c-2 =4v`

`-2 = 4v-c`

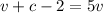
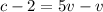
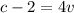
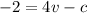
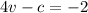`4v-c = -2` --------------------- equation (4)

equating equation (3) and (4); we have:

`6v-c = 6`

`4v-c = -2`

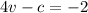
Subtracting equation (3) from (4); we have:

`6v-c = 6`

-
`4v-c = -2`

`2v`
`= 8`

`v=(8)/(2)`

`v=4`

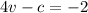
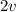
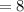
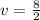
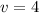
From equation (3); let's replace v=4 in order to solve for c

`6v-c = 6`

6(4) -c = 6

24 -c = 6

-c = 6 - 24

-c = - 18

c = 18

Total number of cupcakes Mercedes bought=v+c

=4+18

=22