Answer:
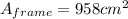
Explanation:
The triangle is attached.
According to the problem, the inner frame is 2 cm wide.
To find the area of that inner frame, we just have to subtract the outer triangle area with the inner triangle area.
Now, we know that the outer part of the triangular canvas has dimensions of 4m, 5m and 7, which are equivalent to 400cm, 500cm, and 700cm, because 1 meter is 100 centimeters.
Now, the area of the other triangle is
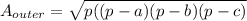
Where
 is half the perimeter. So, if the perimeter is
is half the perimeter. So, if the perimeter is
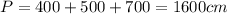
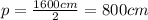
And
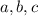 are the sides of the triangle.
are the sides of the triangle.
Replacing all these value, we have
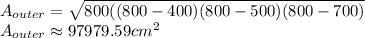
Then, we do the same process, but in this case, the inner canvas has dimensions of 398cm, 498cm and 698 cm.
So, the perimeter is
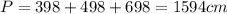
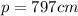
And the area would be
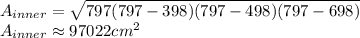
So, the area of the frame is
