Answer:
Perimeter = 21 units
Volume = 110 cubic units
Explanation:
Let the center of circle be (x,y).
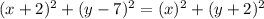
4x - 18y = - 45
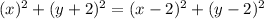
4x + 8y = 4
x + 2y = 1
Solving these 2 equations,
4 - 26y = -45
y =
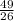
x =
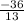
radius = 3.35
Perimeter = 2
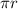 = 21 units
= 21 units
Volume of cylinder =
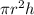
We have to add the volumes of the cylinders.
Volume of smaller cylinder =
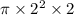 = 8
= 8
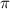
Volume of larger cylinder = 27
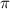
Total volume = 35
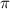 = 110 cubic feet
= 110 cubic feet