Question

Answer these two questions above (in the picture) and PLEASE SHOW YOUR WORK!!

PSA: If you answer me with non sense just to get a few points I’m going to report your account.

Answer 1

sorry, i can only help you with number 6: I believe it would be
`m>n` and that both slopes have the same sign, for the slopes are both negative.

Explanation:

so first, we'll need to find the slope for the linear function, h(x).

use the slope formula which is
`m = \frac{\text{rise}}{\text{run}} = (y_2 - y_1)/(x_2 - x_1)`

where m equals slope and x1, y1, x2, and y2 are coordinate pairs.

so take (-3,1) [this is the x1,y1 pair] and (-2,-2) [this is the x2,y2 pair]

`m=((-2)-1)/((-2)-(-3)) =(-3)/(1) =-3`

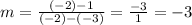
so the slope for h(x) is -3. this means that n equals -3 (for it is the slope of h(x)

we already know that the slope for g(x) is -2, which is also m.

-2 is larger than -3 which would mean that
`m>n`

since both slopes are negative, the 3rd choice would also be true.

hope this helps