Answer:
The graph in the attached figure
Explanation:
we have
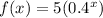
This is a exponential function of the form

where
a is the initial value or the y-intercept of the exponential function
b is the base
b=(1+r)
r is the percent rate of change
we have
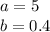
 ---> is a decay function
---> is a decay function
To draw the graph on a piece of paper we will plug in the values of x in the function.
so
For x=-1 --->

For x=0 --->
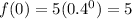
For x=1 --->
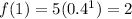
For x=2 --->
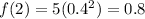
For x=3 --->
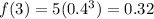
we have the points
(-1,12.5),(0,5),(1,2),(2,0.8),(3,0.32)
Plot the points in a coordinate plane to graph the function
using a graphing tool
The graph in the attached figure
Is a decreasing function, because as x increases (reading from left to right), y decreases