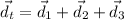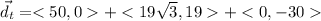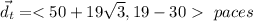Question

You are told to walk due east for 50 paces, then 30 degrees north of east for 38 paces, and then due south for 30 paces. What is the magnitude and direction of your total displacement?​

Answer 1

`\vec d_t=<82.91,-11>\ paces`

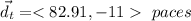
Step-by-step explanation:

Displacement

It's a vectorial magnitude to measure the linear space between two points, It's usually computed as the subtraction of the final point minus the initial point. To find the sum of a sequence of displacements, we must sum the vectors.

In this problem, we see the 'pace' as a unit of length. We'll use it without attempting to convert it to any other standard unit. We'll also assume the positive direction to be east and north in both axes x,y respectively.

The first displacement is 50 paces due east. Let's assume the object starts from the origin (0,0)

Since the displacement is due east, the vertical component is zero, so

`\vec d_1=<50,0>`

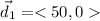
The second displacement is 38 paces 30 degrees north to east. We must find the x and y coordinates of this displacements

`\vec d_2=<38cos30^o,38sin30^o>`

`\vec d_2=<19√(3),19>`

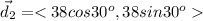
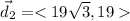
The third displacement is 30 paces due south. This time, the x-coordinate is zero and the y-coordinate is negative

`\vec d_3=<0,-30>`

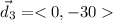
The total displacement is the sum of all three above:

`\vec d_t=\vec d_1+\vec d_2+\vec d_3`

`\vec d_t=<50,0>+<19√(3),19>+<0,-30>`

`\vec d_t=<50+19√(3),19-30>\ paces`