Answer:
Assume that the mass start at a height of
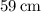 (its equilibrium position.)
(its equilibrium position.)
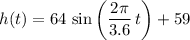 ,
,
where
 is in seconds, and
is in seconds, and
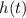 gives the height (in
gives the height (in
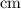 ) of the mass (above the ground.)
) of the mass (above the ground.)
Explanation:
A mass on an ideal, vertical spring is in a simple harmonic motion. Its displacement from its equilibrium
 position at time
position at time
 can be modelled with a sine equation:
can be modelled with a sine equation:
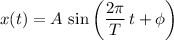 ,
,
where
 is the amplitude of the motion (the difference between the max height and min height.)
is the amplitude of the motion (the difference between the max height and min height.)
 is the time period of the motion.
is the time period of the motion.
 gives the initial (angular) position of the object.
gives the initial (angular) position of the object.
For convenience, assume that
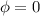 , such that the object starts at equilibrium position.
, such that the object starts at equilibrium position.
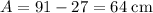 .
.
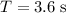 .
.
The equation would become:
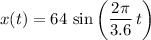 ,
,
The height of the object at equilibrium position is the average between its max and min height.
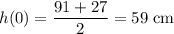 . To find the height of the object, add its height at equilibrium to the displacement from its equilibrium position.
. To find the height of the object, add its height at equilibrium to the displacement from its equilibrium position.
Hence the equation:
 .
.