Question

If a gym class is divided into 4 equal teams, 2 students have to sit out; 5 teams, 1 student has to sit out; 6 teams, 4 students have to sit out. If there are fewer than 70 people in the class, what is the minimum number of students that need to be added so that the class can be divided into 4, 5 and 6 equal teams with no students sitting out?

Answer 1

14 students

Explanation:

Let x be the number of students,
`x<70.`

• If a gym class is divided into 4 equal teams, 2 students have to sit out, so
  `x\equiv 2(\rm mod \ 4);`

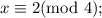
• If a gym class is divided into 5 equal teams, 1 student has to sit out, so
  `x\equiv 1(\rm mod \ 5);`

• If a gym class is divided into 6 equal teams, 4 students have to sit out, so
  `x\equiv 4(\rm mod \ 6).`

From the first congruence,

`x=2+4k,`

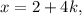
substitute it into the second congruence:

`2+4k\equiv 1(\rm mod\ 5)\\ \\4k\equiv -1(\rm mod\ 5)\\ \\4k\equiv -1+5(\rm mod \ 5)\\ \\4k\equiv 4(\rm mod \ 5)\\ \\k\equiv 1(\rm mod \ 5)\\ \\k=5l+1\\ \\x=4(5l+1)+2=20l+6`

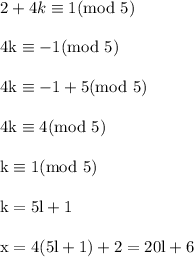
Substitute this into the third congruence:

`20l+6\equiv 4(\rm mod\ 6)\\ \\20l\equiv -2(\rm \ mod 6)\\ \\20l\equiv -2+6\cdot 7(\rm mod\ 6)\\ \\20l\equiv 40(\rm mod \ 6)\\ \\l\equiv 2(\rm mod 6)\\ \\l=6m+2\\ \\x=20(6m+2)+6=120m+46`

Since
`x<70,` then
`x=46\ (\text{when }m=0)`

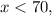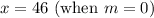
The next number divisible by 4, 5 and 6, greater than 46 and less than 70 is 60, so 14 students should be added.