Answer:
His new time is twice his old time :
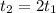
Explanation:
- We need to use an equation that relates speed, distance and time. We are going to use the following equation :
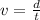
Where ''v'' is the speed
Where ''d'' is the distance
And where ''t'' is the time
- We know by reading the exercise that :
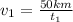 (I)
(I)
Where ''
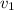 '' is the speed of the first trip and where ''
'' is the speed of the first trip and where ''
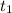 '' is the time of the first trip.
'' is the time of the first trip.
- The equation of the second trip is :
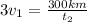 (II)
(II)
Where ''
 '' is the time of the second trip.
'' is the time of the second trip.
- If we use (I) in the equation (II) :
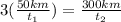 ⇒
⇒

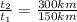
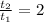
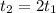
We find that the time of his second trip is twice as the first one.