Question

Drag the tiles to the correct boxes to complete the pairs.

Match the expressions with the nonpermissible replacements for y.
947 97
y(y + 5)
41 +1
5y2 – 6y +
1
-5(y – 1)
32 – 2y + 1
2y - 3

Answer 1

Part 1) -7 →
`(y^2-y+6)/(-2(y+7))`

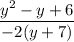
Part 2) 3/2 →
`(y^2-2y+1)/(2y-3)`

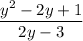
Part 3) 1 →
`(5y^2-6y+1)/(-5(y-1))`

Part 4) -1/4 →
`(y(y+5))/(4y+1)`

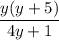
Explanation:

The complete question in the attached figure

we know that

To find out the non permissible replacements for y, equate the denominator of each expression equal to 0.

step 1

we have

`(y^2-2y+1)/(2y-3)`

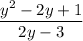
Equate (2y-3) equal to 0.

`2y-3=0`

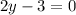
solve for y

Adds 3 both sides.

`2y=3`

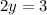
Divide both sides by 2.

`y=(3)/(2)`

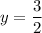
therefore

3/2 is the non permissible replacement for y.

step 2

we have

`(y(y+5))/(4y+1)`

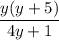
Equate (4y+1) equal to 0.

`4y+1=0`

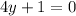
Subtract 1 both sides

`4y=-1`

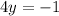
Divide by 4 both sides

`y=-(1)/(4)`

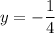
therefore

-1/4 is the non permissible replacement for y.

step 3

we have

`(5y^2-6y+1)/(-5(y-1))`

Equate -5(y-1) equal to 0.

`-5(y-1)=0`

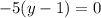
Divide by -5 both sides

`y-1=0`

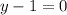
Adds 1 both sides

`y=1`

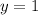
therefore

1 is the non permissible replacement for y.

step 4

we have

`(y^2-y+6)/(-2(y+7))`

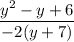
Equate -2(y+7) equal to 0.

`-2(y+7)=0`

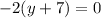
Divide by -2 both sides

`y+7=0`

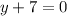
Subtract 7 both sides

`y=-7`

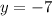
therefore

-7 is the non permissible replacement for y