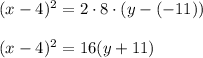Answer:

Explanation:
The directrix is horizontal line and focus is above the directrix, so the equation of the parabola will be in the form
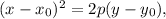
where
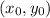 are the coordinates of the vertex.
are the coordinates of the vertex.
The distance between the focus and the directrix is
 units, hence
units, hence
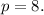
The vertex of the parabola is the point lying halfway from the focus to the directric on vertical line (parabola's axes of symmetry) x = 4, so its coordinates are (4,-11).
Therefore, the equation of parabola is