Answer:
C. Rational
Explanation:
While this number technically has no end, it repeats. This puts it in a special case.
First, lets look at the decimal portion and ignore the integer with it.
When looking at
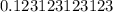 ..., we can convert this into the fraction
..., we can convert this into the fraction
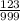
Now, we can multiply -12 by the denominator and add them together to get
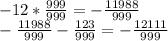
As this number can be written as a fraction, it is a rational number.