Answer:
Question 1:
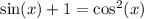
Answer to Question 1:

Question 2:
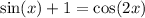
Answer to Question 2:
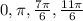
Question:
I will answer the following two questions.
Condition:
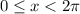
Question 1:
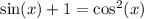
Question 2:
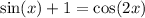
Explanation:
Question 1:
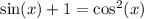
Question 2:
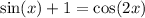
Question 1:
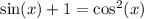
I will use a Pythagorean Identity so that the equation is in terms of just one trig function,
 .
.
Recall
 .
.
This implies that
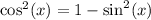 . To get this equation from the one above I just subtracted
. To get this equation from the one above I just subtracted
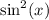 on both sides.
on both sides.
So the equation we are starting with is:
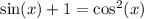
I'm going to rewrite this with the Pythagorean Identity I just mentioned above:
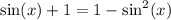
This looks like a quadratic equation in terms of the variable:
 .
.
I'm going to get everything to one side so one side is 0.
Subtracting 1 on both sides gives:
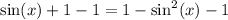
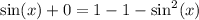

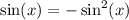
Add
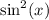 on both sides:
on both sides:
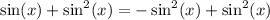
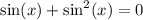
Now the left hand side contains terms that have a common factor of
 so I'm going to factor that out giving me:
so I'm going to factor that out giving me:
![\sin(x)[1+\sin(x)]=0](https://img.qammunity.org/2020/formulas/mathematics/middle-school/ie16o54ymddd5taxu310yoqva93s62r3vv.png)
Now this equations implies the following:
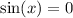 or
or
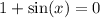
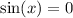 when the
when the
 -coordinate on the unit circle is 0. This happens at
-coordinate on the unit circle is 0. This happens at
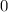 ,
,
 , or also at
, or also at
 . We do not want to include
. We do not want to include
 because of the given restriction
because of the given restriction
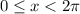 .
.
We must also solve
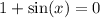 .
.
Subtract 1 on both sides:
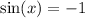
We are looking for when the
 -coordinate is -1.
-coordinate is -1.
This happens at
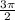 on the unit circle.
on the unit circle.
So the solutions to question 1 are
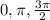 .
.
Question 2:
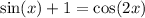
So the objective at the beginning is pretty much the same. We want the same trig function.
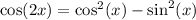 by double able identity for cosine.
by double able identity for cosine.
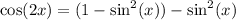 by Pythagorean Identity.
by Pythagorean Identity.
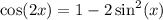 (simplifying the previous equation).
(simplifying the previous equation).
So let's again write in terms of the variable
 .
.
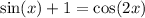
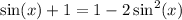
Subtract 1 on both sides:
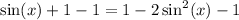
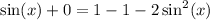
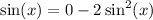

Add
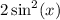 on both sides:
on both sides:
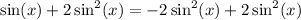
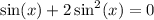
Now on the left hand side there are two terms with a common factor of
 so let's factor that out:
so let's factor that out:
![\sin(x)[1+2\sin(x)]=0](https://img.qammunity.org/2020/formulas/mathematics/middle-school/qa7l5pzskezuyvw891a9iiv1s8t3g7jl7x.png)
This implies
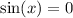 or
or
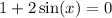 .
.
The first equation was already solved in question 1. It was just at
 .
.
Let's look at the other equation:
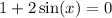 .
.
Subtract 1 on both sides:

Divide both sides by 2:
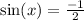
We are looking for when the
 -coordinate on the unit circle is
-coordinate on the unit circle is
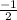 .
.
This happens at
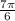 or also at
or also at
 .
.
So the solutions for this question 2 is
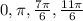 .
.