Question

If the sum of two positive numbers x and y is 3, then the absolute maximum of x^3+12xy is what?

Answer 1

32 at x = 2

Explanation:

If the sum of two positive numbers x and y is 3, then

`x+y=3\Rightarrow y=3-x`

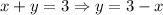
and

`x^3+12xy=x^3+12x(3-x)=x^3-12x^2+36x`

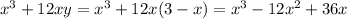
To find the absolute maximum of the function

`f(x)=x^3-12x^2+36x`

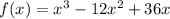
find the derivative

`f'(x)=3x^2-24x+36`

and equate it to 0:

`3x^2-24x+36=0\\ \\x^2-8x+12=0\\ \\D=(-8)^2-4\cdot 12=64-48=16\\ \\x_(1,2)=(-(-8)\pm √(16))/(2\cdot 1)=(8\pm 4)/(2)=6,\ 2`

For
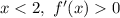`x<2,\ f'(x)>0` - the function f(x) increases

For
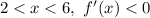`2<x<6,\ f'(x)<0` - the function f(x) decreases

For
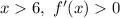`x>6,\ f'(x)>0` - the function f(x) increases

So, x = 2 is maximum, x = 6 is minimum

The maximum value of
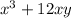`x^3+12xy` is

`2^3+12\cdot 2\cdot (3-2)=8+24=32`