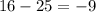Question

Help me plz!!! Wanna know the answer of (d). Thank you so much!!!!

Answer 1

d = -9

Explanation:

First lets input our x value for g(x)

This gives us the integral

`g(6) = \int\limits^6_(-4) {f(x)} \, dx`

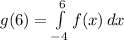
First, we need to split this integral into the different aspects of the piecewise function. This will give us

`g(6)=\int\limits^0_(-4) {4} \, dx +\int\limits^5_0 {-5} \, dx +\int\limits^6_5 {0} \, dx`

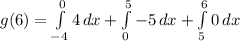
Now, we need to evaluate each of these integrals

`\int\limits^0_(-4) {4} \, dx=4x|\limits^0_(-4)\\\\4(0)-4(-4)=16`

`\int\limits^5_0 {-5} \, dx=-5x|\limits^5_0\\\\-5(5)--5(0)\\\\-25`

`\int\limits^6_5 {0} \, dx=0`

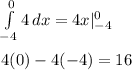
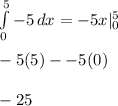
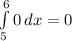
Now all we need to do is add the values of each of these integrals

`16-25=-9`