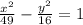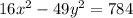Answer:
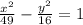 is the equation of hyperbola.
is the equation of hyperbola.
Explanation:
Given:
Vertices of the hyperbola: (-7,0) and (7,0)
Co-vertices of the hyperbola: (0,-4) and (0,4)
Mid-point of the vertices = center of hyperbola = (0,0)
Focii lie on the same line as vertices and hence they lie on x-axis.
Here x-axis is the tranverse axis and y-axis is the conjugate axis.
length of semi-transverse axis = a = 7
length of semi-conjugate axis = b = 4
Equation of hyperbola is of the form:
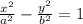
Substituting a = 7 and b = 4 we get: