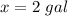Question

An art museum has a pentagon-shaped room. When drawn to scale on a coordinate grid, the corners of the room are points (18,20):

B(4,20): C(4,4): D(16.2): E(22.10), shown in feet. The walls are 10 feet high.
The museum is going to paint four of the walls: AB, BC, DE, and AE. Assume one gallon of paint is enough to cover 400 square feet.
How many gallons of paint should the museum purchase? Enter your answer as a whole number.

Answer 1

`2\ gal`

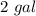
Explanation:

we know that

the formula to calculate the distance between two points is equal to

`d=\sqrt{(y2-y1)^(2)+(x2-x1)^(2)}`

we have

`A(18,20),B(4,20),C(4,4),D(16.2),E(22.10)`

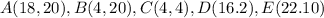
step 1

Find the distance AB

we have

`A(18,20),B(4,20)`

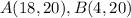
substitute in the formula

`d=\sqrt{(20-20)^(2)+(4-18)^(2)}`

`d=\sqrt{(0)^(2)+(-14)^(2)}`

`AB=14\ ft`

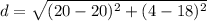
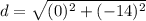
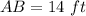
step 2

Find the distance BC

we have

`B(4,20),C(4,4)`

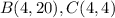
substitute in the formula

`d=\sqrt{(4-20)^(2)+(4-4)^(2)}`

`d=\sqrt{(-16)^(2)+(0)^(2)}`

`BC=16\ ft`

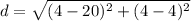
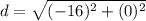
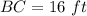
step 3

Find the distance DE

we have

`D(16.2),E(22.10)`

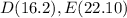
substitute in the formula

`d=\sqrt{(10-2)^(2)+(22-16)^(2)}`

`d=\sqrt{(8)^(2)+(6)^(2)}`

`d=√(100)`

`DE=10\ ft`

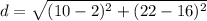
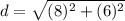
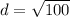
step 4

Find the distance AE

we have

`A(18,20),E(22.10)`

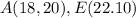
substitute in the formula

`d=\sqrt{(10-20)^(2)+(22-18)^(2)}`

`d=\sqrt{(-10)^(2)+(4)^(2)}`

`d=√(116)`

`AE=10.77\ ft`

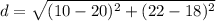
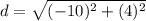
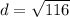
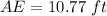
step 5

Find out the area of the four walls

To determine the area sum the length sides and multiply by the height of the walls

so

`A=(AB+BC+DE+AE)h`

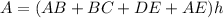
substitute the given values

The height of the walls is 10 ft

`A=(14+16+10+10.77)10`

`A=(50.77)10`

`A=507.7\ ft^2`

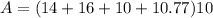
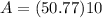
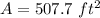
step 6

Determine the number of gallons needed to paint the four walls

we know that

one gallon of paint is enough to cover 400 square feet

using proportion

`(1)/(400)\ (gal)/(ft^2)=(x)/(507.7)\ (gal)/(ft^2)\\\\x=507.7/400\\\\x= 1.27\ gal`

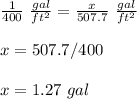
Round up

`x=2\ gal`