Question

A 12-year, 5% coupon bond pays interest annually. What is the change in the price of this bond if the market yield rises to 6% from the current yield of 4.5%?

Answer 1

There will the decrease of 12.38% in the price of bond.

Step-by-step explanation:

Assume that the face value of bond is $1,000. The 5% coupon payments will product annuity (constant annual payments) of $50 (5% x $1,000) each year for next 12 years.

1. Currently, the yield (or the required rate of return in simple words) is the 4.5%. At this rate, value of bond can be computed as follows:

• Present value interest payments:

= 50 * Present value of annuity (at n= 12, i= 4.5%)

(Refer to table of PVIFA in your text book to find the factor at n=12 and i = 4.5%)

= 50 * 9.11

= $455.5

• Present value of principal payment at maturity:

=
`1000*(1)/((1+0.045)^12)`

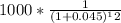
= $586.6

Hence, the value of bond at 4.5% yield is equal to $455.5 + $586.6 = $1,045.1

2. Now, the yield is 6%. At this rate, value of bond can be computed as follows:

• Present value interest payments:

= 50 * Present value of annuity (at n= 12, i= 6%)

(Refer to table of PVIFA in your text book to find the factor at n=12 and i = 6%)

= 50 * 8.384

= $419.2

• Present value of principal payment at maturity:

=
`1000*(1)/((1+0.06)^12)`

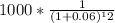
= $496.96

Hence, the value of bond at 6% yield is equal to $419.2 + $496.96 = $916.88

Finally, the percentage between the final value of bond ($916.88) and the initial value of bond ($1,045.1) will be the decrease of 12.38% in price.