Question

A car drives horizontally off a 83-m-high cliff at a speed of 25 m/s . Ignore air resistance. Part A How long will it take the car to hit the ground? How long will it take the car to hit the ground?

a.4.9 s
b.4.5 s
c.4.1 s
d.2.7 s
e.5.7 s

Answer 1

c. 4.1 s

Explanation:

We have been given that a car drives horizontally off a 83-m-high cliff at a speed of 25 m/s . Ignore air resistance.

To solve our given problem, we will use free fall formula. The free fall formula states that the distance the object falls, or height, h, is 1/2 gravity times the square of the time falling.

`h=(1)/(2)gt^2`

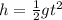
Solve for t:

`2*h=2*(1)/(2)gt^2`

`2h=gt^2`

`(2h)/(g)=(gt^2)/(g)`

`(2h)/(g)=t^2`

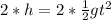
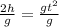
Switch sides:

`t^2=(2h)/(g)`

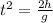
Take positive square root:

`t=\sqrt{(2h)/(g)}`

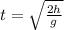
In our given situation
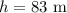`h=83\text{ m}`. We know
`g=9.81(m)/(s^2)`.

`t=\sqrt{(2(83m))/(9.81(m)/(s^2))}`

`t=\sqrt{(166)/(9.81)s^2}`

`t=√(16.9215086646279307s^2)`

`t=4.113576140s`

`t\approx 4.1s`

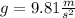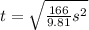
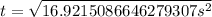
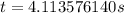
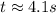
Therefore, it will take 4.1 seconds the car to hit the ground and option 'c' is the correct choice.