Let
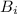 denote the value on the
denote the value on the
 -th drawn ball. We want to find the expectation of
-th drawn ball. We want to find the expectation of
 , which by linearity of expectation is
, which by linearity of expectation is
![E[S]=E\left[\displaystyle\sum_(i=1)^5B_i\right]=\sum_(i=1)^5E[B_i]](https://img.qammunity.org/2020/formulas/mathematics/college/e5vvw5bzgzg5ftmpv6b8crrj442pep7an9.png)
(which is true regardless of whether the
 are independent!)
are independent!)
At any point, the value on any drawn ball is uniformly distributed between the integers from 1 to 10, so that each value has a 1/10 probability of getting drawn, i.e.
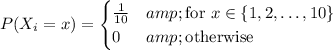
and so
![E[X_i]=\displaystyle\sum_(i=1)^(10)x\,P(X_i=x)=\frac1{10}\frac{10(10+1)}2=5.5](https://img.qammunity.org/2020/formulas/mathematics/college/igmzyta7nq1m5j7c50uboeo8colr53ac24.png)
Then the expected value of the total is
![E[S]=5(5.5)=\boxed{27.5}](https://img.qammunity.org/2020/formulas/mathematics/college/aedlng2jfjgns59efb977cpofc6641k4xg.png)