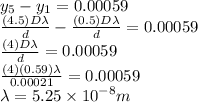Answer:

Step-by-step explanation:
 = separation of the slits = 0.21 mm = 0.00021 m
= separation of the slits = 0.21 mm = 0.00021 m
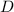 = Screen distance = 59 cm = 0.59 m
= Screen distance = 59 cm = 0.59 m
 = wavelength of the light
= wavelength of the light
tex]y_{n}[/tex] = location of nth minima on the screen
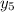 = location of fifth minima on the screen
= location of fifth minima on the screen
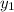 = location of first minima on the screen
= location of first minima on the screen
location of nth minima on the screen is given as

For n = 1
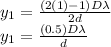
For n = 5
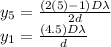
Given that: