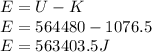Question

A 64 kg sky diver jumped out of an airplane at an altitude of 0.90 km. She opened her parachute after a while and eventually landed on the ground with a speed of 5.8 m/s. How much energy was dissipated by air resistance during the jump?

Answer 1

563403.5 J

Step-by-step explanation:

`m` = mass of the skydiver = 64 kg

`h` = Altitude of the airplane = 0.90 km = 900 m

`v` = speed at the time of landing = 5.8 m/s

Gravitational potential energy of the skydiver at the airplane is given as

`U = mgh\\U = (64) (9.8) (900)\\U = 564480 J`

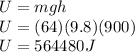
Kinetic energy of the skydiver at the time of landing is given as

`K = (0.5) m v^(2) = (0.5) (64) (5.8)^(2) = 1076.5 J`

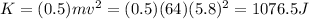
`E` = Energy dissipated by air resistance

Energy dissipated by air resistance during the jump is given as

`E = U - K \\E = 564480 - 1076.5\\E = 563403.5 J`