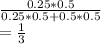Question

(a) Let {A1, A2} be a partition of a sample space and let B be any event. State and prove the Law of Total Probability as it applies to the partition {A1, A2} and the event B.

There are two coins in a box; one coin is a fair coin, and the other is a biased coin thatcomes up heads 75 percent of the time. Fiona chooses a coin at random and tosses it.
(b) What is the probability that the chosen coin flips heads? (Hint: The Law of TotalProbability.)
(c) Given that the chosen coin flips heads, what is the conditional probability that it wasthe biased coin? (Hint: Bayes’ Theorem.)
(d) Given that the chosen coin flips tails, what is the conditional probability that it wasthe biased coin?

Answer 1

0.625

Explanation:

Given that {A1, A2} be a partition of a sample space and let B be any event. State and prove the Law of Total Probability as it applies to the partition {A1, A2} and the event B.

Since A1 and A2 are mutually exclusive and exhaustive, we can say

b) P(B) = P(A1B)+P(A2B)

Selecting any one coin is having probability 0.50. and A1, A2 are events that the coins show heads.
`P(B/A1) = 0.50 \\P(B/A2) = 0.75\\P(A1B) = 0.5(0.5) = 0.25 \\P(A2B) = 0.75(0.5) = 0.375\\P(B) = 0.625`

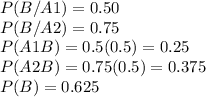
c) Using Bayes theorem

conditional probability that it wasthe biased coin

=
`(0.375)/(0.625) \\=(3)/(5)`

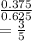
d) Given that the chosen coin flips tails,the conditional probability that it was the biased coin=
`(0.25*0.5)/(0.25*0.5+0.5*0.5) \\=(1)/(3)`