Question

A railway car having a total mass of 5.8 × 105 kg, moving with a speed of 9.1 km/h, strikes another car that has a mass of 8.7 × 105 kg and is initially at rest. The speed of the coupled cars after the collision is

A) 9.1 km/h.
B) 7.2 km/h.
C) 3.6 km/h.
D) 1.8 km/h.
E) 4.2 km/h

Answer 1

Final speed of both the cars, V = 3.28 km/h

Step-by-step explanation:

It is given that,

Mass of the railway car,
`m_1=5.8* 10^5\ kg`

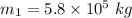
Initial speed of the railway car,
`u_1=9.1\ km/h=2.52\ m/s`

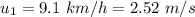
Mass of another car,
`m_2=8.7* 10^5\ kg`

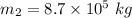
Initial speed of another car,
`u_2=0`

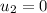
To find,

The speed of the coupled cars after the collision.

Solution,

It is a case of inelastic collision in which the linear momentum before and after the collision remains same. Let V is the coupled velocity of both of the cars. So,

`m_1u_1+m_2u_2=(m_1+m_2)V`

`V=(m_1u_1+m_2u_2)/((m_1+m_2))`

`V=(m_1u_1)/((m_1+m_2))`

`V=(5.8* 10^5* 2.52778)/((5.8* 10^5+8.7* 10^5))`

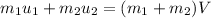
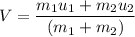
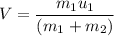
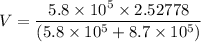
V = 1.011 m/s

or

V = 3.28 km/h

So, the speed of the coupled cars after the collision is 3.28 km/h. Hence, this is the required solution.