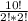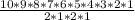Question

What is the number of distinct permutations that can be formed from all the letters of the word CALIFORNIA? In the supplied answer choices, ! denotes factorial.

Answer 1

The answer is "907,200".

Step-by-step explanation:

In the word CALIFORNIA, there is a total of 10 letters in which letter A and Letter I is repeated 2 times. To solve this problem we use the multinomial principle.

The multinomial distribution model shows the results of n trials where the results of each study are prescriptive. It is also known as a distribution that makes the binomial distribution generalizable.

Ex:

`(10!)/(2!*2!)`

`(10*9*8*7*6*5*4*3*2*1)/(2*1*2*1)`

`(10*9*8*7*6*5*4*3*2*1)/(4)`

`10*9*8*7*6*5*3*2*1=907,200`