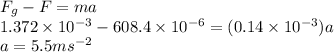Answer:
A)
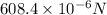
B)
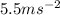
Step-by-step explanation:
A)
 = magnitude of charge on each sphere =
= magnitude of charge on each sphere =
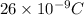
 = Distance between the two spheres = 10 cm = 0.10 m
= Distance between the two spheres = 10 cm = 0.10 m
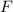 = magnitude of force between the two spheres
= magnitude of force between the two spheres
Using Coulomb's law, magnitude of the force between two charged sphere
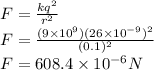
B)
 = mass of the sphere =
= mass of the sphere =
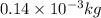
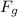 = Force of gravity in down direction =
= Force of gravity in down direction =

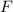 = Electrostatic force of repulsion in upward direction =
= Electrostatic force of repulsion in upward direction =
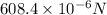
 = acceleration of the sphere
= acceleration of the sphere
Force equation for the motion of the sphere is given as