Question

For the relation given, do the following:

1. state whether the relation is reÒexive (2 pts)
2. state whether the relation is symmetric (2 pts)
3. state whether the relation is transitive (3 pts)
If the relation is NOT (reflexive, symmetric, transitive), you must give a counterexample that proves it.R3 = { (0,0), (0,1), (0,2), (1,2) }

Answer 1

1.No

2.No

3.Transitive

Explanation:

We are given that a relation

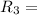`R_3=`{(0,0),(0,1),(0,2),(1,2)}

If a relation is reflexive then (a,a) belongs to relation for each a belongs to given set.

A relation is symmetric

If (a,b)
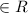`\in R` then,
`(b,a)\in R`

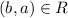
A relation is transitive

(a,b) and (b,c)
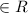`\in R` then, (a,c)
`\in R`

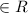
1.The relation is not reflexive because (1,1) does not belongs to
`R_3`

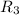
2.The relation is not symmetric because (2,0)
`in R_3`

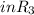
3.It is transitive because (0,1) and (1,2)
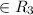`\in R_3` then (0,2)[tex\in R_3[/tex]