Question

It takes 4.0 eV to excite an electron in a box from the ground level to the first excited level. What is the width L of the box?

A. 0.27 mm
B. 0.11 nnm
C. 0.53 nm
E. 38.8 cnm

Answer 1

To solve this problem we will use the concept related to electrons in a box which determines the energy of an electron in that state.

Mathematically this expression is given by,

`E_n= (n^2h^2)/(8mL^2)`

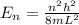
Where,

m = mass of an electron

h = Planck's constant

n = is the integer number of the eigenstate

L = Quantum well width

The change in energy must be given in state 1 and 2, therefore

`\Delta E = E_2 - E_1`

`\Delta E = (2^2h^2)/(8mL^2)-(1^2h^2)/(8mL^2)`

`\Delta E = (3h^2)/(8mL^2)`

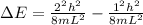
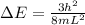
Replacing we have:

`(4*1.6*10^(-19)) = (3(6.626*10^(34)))/(8*(9.11*10^(-31))*L^2)`

`L = 0.53nm`

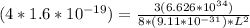
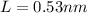
Therefore the correct answer is C.