Question

Calculate the energy E (in MeV) released in the following nuclear fission reaction: 242 Am + X → 90 Sr + 149 La + 4 n Start by completing the reaction, and use the following nuclear masses: 242 Am = 242.0595490 u, 90 Sr = 89.9077387 u, and 149 La = 148.934733 u. The symbol X represents an unknown particle.

Answer 1

177.993 MeV

Step-by-step explanation:

Nuclear fission refers to a process where a nucleus is broken into smaller ones.

m(Am) = 242.0595490 u, m(Sr) = 89.9077387 u, m(La) = 148.934733 u and m(n) = 1.008665 u. To find the mass of X, we sum up the masses on both side and subtract them according to the equation given

242 + X = 90 +149 + 4

X = 243 - 242 = 1

so X is a neutron

next we calculate the Δm ( change in mass)

Δm = mass reactant - mass of product

(242.0595490 + 1.008665 ) - ( 89.9077387 + 148.934733 + 4 (1.008665))

= 243.068214 - 242.8771317 = 0.1910823 u

using the formula

E = (Δm) c² = 0.1910823 u × c² ×
`(931.5MeV)/(c^2)`×
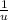`(1)/(u)` = 177.993 MeV