Question

A spherical balloon is deflating at 10 cm3/s. At what rate is the radius changing when the volume is 1000π cm3 ? What is the rate of change of surface area at this moment?

Answer 1

1.dr/dt=0.0096cm/s

2. dA/dt=2.19cm^2/s

Step-by-step explanation:

A spherical balloon is deflating at 10 cm3/s. At what rate is the radius changing when the volume is 1000π cm3 ? What is the rate of change of surface area at this moment?

for this question, we need to analyze the parameters we know

V=volume of the spherical balloon 1000π cm3

volume of the sphere=
`(4)/(3) \pi r^(3)`

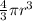
1000π=4/3πr^3

dividing both sides by 4

250*3=r^3

r=9.08cm, the radius of the balloon

dv/dt=dv/dr*dr/dt...................................1

dv/dr ,means

V=
`(4)/(3) \pi r^(3)`

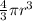
dv/dr=4*pi*r^2

dv/dt=10 cm3/s

from equ 1

10=4*pi*9.08^2*dr/dt

10=1036 dr/dt

dr/dt=10/1036

dr/dt=0.0096cm/s

2. to find the rate at which the area is changing we have,

dA/dt=dA/dr*dr/dt

area of a sphere is 4πr^2

differentiate a with respect to r, radius

dA/dr=8πr

dA/dt=8πr*0.0096

dA/dt=8*pi*9.08*0.0096

dA/dt=2.19cm^2/s

is the rate of change of the surface area