Answer:
t = 1.068 s
Explanation:
given,
a(t) =- k v(t)
speed of the object decreases from 800 ft/s to 700 ft/s
distance = 1400 ft
time for deceleration = ?
a(t) =- k v(t)
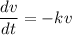
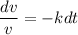
integrating both side
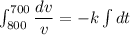
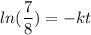
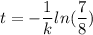 ..........(1)
..........(1)
since,
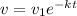
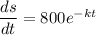
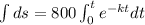
![1400= -(800)/(k)[e^(-kt)-e^0]](https://img.qammunity.org/2020/formulas/mathematics/college/1cizq9cyupgxrvqghi7abbcfoiskktg160.png)
from equation 1
![k= -(8)/(14)[(7)/(8)-1]](https://img.qammunity.org/2020/formulas/mathematics/college/bxsk88yjs8o2tihrt9p4vmemau4g49epok.png)
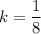
putting value of k in equation (1)
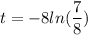
t = 1.068 s