Answer:
Width:
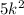 ,
,
Length:
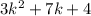
Explanation:
Consider the question: The rectangle below has an area of
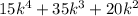 square meters
square meters
. The width of the rectangle (in meters) is equal to the greatest common monomial factor of
 and
and
 . What is the length and width of the rectangle ?
. What is the length and width of the rectangle ?
First of all, we will find the greatest common monomial factor of
 and
and
 to determine the width as:
to determine the width as:
The greatest common factor of number part is 15, 20 and 35 is 5. The greatest common factor of variable part
 is
is
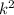 .
.
Since the greatest common monomial factor of
 and
and
 is
is
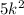 , therefore, the width of the given rectangle is
, therefore, the width of the given rectangle is
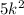 meters.
meters.
Since area of rectangle is product of length and width of rectangle, so we will divide area of given rectangle by width
 to find the length of rectangle:
to find the length of rectangle:
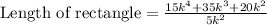
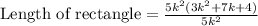
Cancel out common factors:
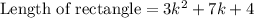
Therefore, the length of the given rectangle is
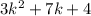 meters.
meters.