Question

Describe how to transform the graph of f into the graph of g. f(x) = x4 and g(x) = -(-x)4 Reflect the graph of f across the x-axis and then reflect across the y-axis. Shift the graph of f down 1 unit. Reflect the graph of f across the x-axis. Reflect the graph of f across the y-axis.

Answer 1

Answer: First option.

Explanation:

Below are shown some transformations for a function
`f(x)`:

- If
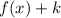`f(x)+k`, the function is shifted up "k" units.

- If
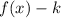`f(x)-k`, the function is shifted down "k" units.

- If
`-f(x)`, the function is reflected across the x-axis.

- If
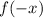`f(-x)`, the function is reflected across the y-axis.

In this case the exercise provides you the following parent function:

`f(x)=x^4`

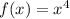
And the function g(x):

`g(x) = -(-x)^4`

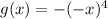
Knowing that the graph of the function
`g(x)` is the graph of the function
`f(x)` transformed, you can identify that the transformations is:

`g(x)=-f(-x)`

Therefore, based on the transformations explained at the beginning, to transform the graph of
`f(x)` to the graph of
`g(x)` you must: Reflect the graph of
`f(x)` across the x-axis and then reflect it across the y-axis.