Question

Consider two point charges located on the x axis: one charge, q1= -11.0 nC, is located at x1= -1.675 m; the second charge, q2= 31.0 nC, is at the origin (x=0.0000).

What is the net force exerted by these two charges on a third charge q3= 47.5 nC placed between q1 and q2 at x3= -1.180 m?

Your answer may be positive or negative, depending on the direction of the force.

Answer 1

Please refer to the figure.

q1 is a negative charge, and q2 and q3 are positive charges. So, the force exerted by q1 on q3 is attractive, and the force exerted by q2 on q3 is repulsive, which means F13 is directed towards left, and F23 is also directed towards left.

`F_(13) = (1)/(4\pi \epsilon_0)(q_1 q_3)/(r_1^2) = (1)/(4\pi \epsilon_0)(11* 10^(-9)* 47.5*10^(-9))/((-1.675 - (-1.18))^2) = 1.92* 10^(-5)N`

`F_(23) = (1)/(4\pi\epsilon_0)(q_2q_3)/(r_2^2) = (1)/(4\pi\epsilon_0)(31* 10^(-9) * 47.5* 10^(-9))/((-1.18 - 0)^2) = 9.5* 10^(-6)`

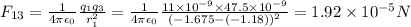
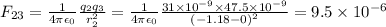
The net force on q3 is the sum of these two forces:

`F_(net) = F_(13) + F_(23) = -1.92* 10^(-5) + (-19.5*10^(-6)) = 2.8* 10^(-5) N`

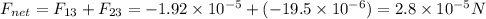
Since both forces are directed towards left, their sign should be negative.