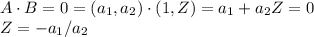Question

Determine the vector expression for the perpendicular component of one vector relative to another vector.

Answer 1

The expression of the perpendicular vector to vector A and B, been A = (a₁ , a₂ , a₃) and B = ( b₁ , b₂ , b₃ ), is ( a₂b₃ -a₃b₂ , a₃b₁ -a₁b₃ , a₁b₂- a₂b₁) in a three dimensional space.

The expresion for the perpendicular vector of A = (a₁,a₂) in 2D is (1, -a₁/a₂)

Step-by-step explanation:

If you want a perpendicular vector to another two known ones, been in a three-dimensional Cartesian coordinate system, you have to make a cross product between the 2 known vectors:

`A\wedge B=Det\left[\begin{array}{ccc}X&Y&Z\\a1&a2&a3\\b1&b2&b3\end{array}\right]`

If you want a perpendicular vector to another known one, been in a two-dimensional Cartesian coordinate system, you can propose a vector B=(1,z) and consider than Dot product A·B = 0. Therefore:

`A\cdot B = 0 = (a_(1) ,a_(2))\cdot (1,Z) = a_(1)+a_(2)Z=0\\Z=-a_(1)/a_(2)`