Question

For the situation below determine the independent value, the dependent value, and the constant of proportionality for both ratios. Confirm your calculations by setting up a proportion with the two ratios and then cross-multiplying.

A package of 7 steaks costs $44.10. A package of 11 steaks costs $69.30.

Answer 1

see the explanation

Explanation:

we know that

A relationship between two variables, x, and y, represent a proportional variation if it can be expressed in the form
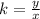`k=(y)/(x)` or
`y=kx`

Let

x ----> the number of steaks in the package

y ----> the cost

In this problem

The independent value or input value is the number of steaks (variable x)

The dependent value or output value is the cost (variable y)

In a proportional relationship the constant of proportionality k is equal to the slope m of the line and the line passes through the origin

so

`k=(y)/(x)`

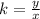
First ratio

x=7, y=44.10 ---->
`k=(44.10)/(7)\ \$/steak`

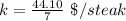
Second ratio

x=11, y=69.30 ---->
`k=(69.30)/(11)\ \$/steak`

Verify the proportions

`(44.10)/(7)=(69.30)/(11)`

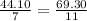
cross-multiplying

`44.10(11)=69.30(7)`

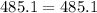`485.1=485.1` ---> is true

therefore

The relationship between the variables, x, and y, represent a proportional variation