Answer:
The answer is B) 0.57.
Explanation:
In this problem we have to apply queueing theory.
It is a single server queueing problem.
The arrival rate is
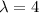 and the service rate is
and the service rate is
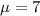 .
.
The proportion of time that the server is busy is now as the "server utilization"and can be calculated as:
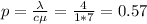
where c is the number of server (in this case, one server).