Answer:
the P matrix you are looking for is P=(1/
 ) · [[1 1 0 0],[1 -1 0 0],[0 0 1 1],[0 0 1 -1]]
) · [[1 1 0 0],[1 -1 0 0],[0 0 1 1],[0 0 1 -1]]
Explanation:
Answer:
For an orthogonal diagonalization of any matrix you have to:
1º) Find the matrix eigenvalues in a set order.
2º) Find the eigenvectors of each respective eigenvalues.
Tip: You can write the matrix A like A =
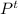 D P
D P
3º) D is the diagonal matrix with each eigenvalue (in order) in the diagonal.
4º) Write P as the normalized eigenvectors in order (in columns).
Tip 2: Remember,
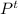 ·P = I, so if A =
·P = I, so if A =
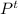 D P, then:
D P, then:
P A
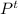 = P
= P
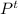 D P
D P
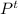 = I D I = D
= I D I = D
So the P we are looking for is the
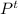 of the diagonalization.
of the diagonalization.
Tip 3: In this case, A is a block matrix with null nondiagonal submatrixes, therefore its eigenvalues can be calculated by using the diagonal submatrixes. The problem is reduced to calculate the eigenvalues of A₁₁ = A ₂₂ = [[5 3],[3 5]]
Solving:
1º)the eigenvalues of A₁₁ are {8,2}, therefore the D matrix is
![\left[\begin{array}{cccc}8&0&0&0\\0&2&0&0\\0&0&8&0\\0&0&0&2\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/8cvbwqn05s0aojcbx8biawqpgjz1x73g7t.png)
2º) the eigenvectors of A₁₁ are P₈= {[1 1]T} P₂= {[1 -1]T}, therefore normalizing the eigenvectors you obtain P = (1/
 ) · [[1 1 0 0],[1 -1 0 0],[0 0 1 1],[0 0 1 -1]] (you can see that P =
) · [[1 1 0 0],[1 -1 0 0],[0 0 1 1],[0 0 1 -1]] (you can see that P =
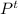 in this case).
in this case).
As said in "tip 2": P A
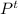 = P
= P
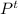 D P
D P
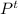 = I D I = D
= I D I = D
So the P obtained is the one you are looking for.