Question

If we fail to reject the null hypothesis in a test using analysis of variance, we are concluding that

a.the populations from which our samples come are the same.
b.the samples are dependent.
c.the sample means are different.
d.the population variances are the different.

Answer 1

On this case if we FAIL to reject the null hypothesis we are concluding that all the population means are equal, so the best option for this case is:

a.the populations from which our samples come are the same.

Explanation:

Previous concepts

Analysis of variance (ANOVA) "is used to analyze the differences among group means in a sample".

The sum of squares "is the sum of the square of variation, where variation is defined as the spread between each individual value and the grand mean"

Solution to the problem

If we have j gtoups, the hypothesis for this case is:

Null hypothesis:
`\mu_(1)=\mu_(2)=......=\mu_(j)`

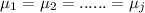
Alternative hypothesis: Not all the means are equal
`\mu_(i)\\eq \mu_(j), i,j=1,2,....,j`

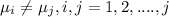
If we assume that we have
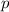`p` groups and on each group from
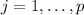`j=1,\dots,p` we have
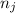`n_j` individuals on each group we can define the following formulas of variation:

`SS_(total)=\sum_(j=1)^p \sum_(i=1)^(n_j) (x_(ij)-\bar x)^2`

`SS_(between)=SS_(model)=\sum_(j=1)^p n_j (\bar x_(j)-\bar x)^2`

`SS_(within)=SS_(error)=\sum_(j=1)^p \sum_(i=1)^(n_j) (x_(ij)-\bar x_j)^2`

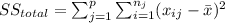
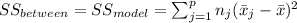
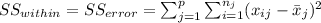
And we have this property

`SST=SS_(between)+SS_(within)`

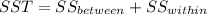
On this case if we FAIL to reject the null hypothesis we are concluding that all the population means are equal, so the best option for this case is:

a.the populations from which our samples come are the same.