Answer:
The correct option is: C. 250 K
Step-by-step explanation:
Given: Before Sublimation-
Initial Temperature: T₁ = 300 K, Initial Pressure: P₁ = 1 atm, Initial number of moles of gas: n₁ = 1 mol, given mass of solid Carbon dioxide: w = 88 g
After Sublimation-
Final Pressure: P₂ = 2.5 atm, Final number of moles of gas: n₂ = ? mol
Final Temperature: T₂ = ? K,
Also, Volume is constant, Molar mass of Carbon dioxide: m = 44 g/mol
As we know,
The number of moles:
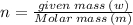
So the number of moles of carbon dioxide sublimed:
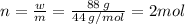
Therefore, the final number of moles of gas after sublimation:
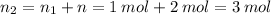
According to the Ideal gas equation:
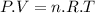
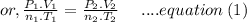
Since the volume is constant, so the equation (1) can be written as:
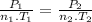
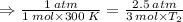
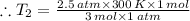

Therefore, the final temperature: T₂ = 250 K