Question

Prove that T is one to one if and only if T carries linearly independent subsets of V onto linearly independent subsets of W.

Answer 1

Answer with Step-by-step explanation:

Suppose T is one-one

Let S be a linearly independent subset of V

We want to show that T(S) is linearly independent.

Suppose T(S) is linearly dependent.

Then there exist
`v_1,v_2,...v_n\in S` and some not all zero scalars
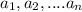`a_1,a_2,....a_n` such that

`a_1T(v_1)+a_2T(v_2)+a_3T(v_3)+...+a_nT(v_n)=0`

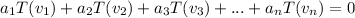
T is linear therefore,

`T(a_1v_1+a_2v_2+..+a_nv_n)=0`

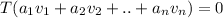
T is one-one therefore

N(T)=0

`a_v_1+....+a_nv_n=0`

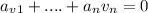
S is linearly independent therefore,

`a_1=a_2=...a_n=0`

It is contradiction.Hence, T(S) is linearly independent.

Conversely, Suppose that T carries linearly independent subset of V onto linearly independent subsets of W.

Assume that T(x)=0 if the set x is linearly independent

Then, by assumption we conclude that {0} is linearly independent but {0} is linearly dependent.

It is contradiction .Hence, the set {x} is linearly dependent which implies that x=0

It means N(T)={0}.Therefore, T is one- one