Question

A wire of radius R has a current I uniformly distributed across its cross-sectional area. Ampere's law is used with a concentric circular path of radius r, with r < R, to calculate the magnitude of the magnetic field B.

Answer 1

Please refer to the figure.

Step-by-step explanation:

The crucial point here is to calculate the enclosed current. If the current I is flowing through the whole cross-sectional area of the wire, the current density is

`J = (I)/(\pi R^2)`

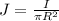
The current density is constant for different parts of the wire. This idea is similar to that of the density of a glass of water is equal to the density of a whole bucket of water.

So,

`J = (I)/(\pi R^2) = (I_(enc))/(\pi r^2)\\I_(enc) = (Ir^2)/(R^2)`

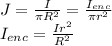
This enclosed current is now to be used in Ampere’s Law.

`\mu_o I_(enc) = \int {B} \, dl`

Here,
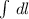`\int \, dl` represents the circular path of radius r. So we can replace the integral with the circumference of the path,
`2\pi r`.

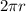As a result, the magnetic field is

`B = (\mu_0)/(2\pi)(Ir)/(R^2)`