Question

laura has a mass of 60kg and is sitiing 265cm from the fulcrum of a seesaw. bill has a mass of 50kg. how far from the fulcrum must he be to balance the seesaw?

Answer 1

318 cm.

Explanation:

Let x represent the distance between Bill and fulcrum.

We have been given that Laura has a mass of 60 kg and is sitting 265 cm from the fulcrum of a seesaw. Bill has a mass of 50 kg.

To balance the seesaw, the product of Laura's weight and her distance from fulcrum of seesaw should be equal to the product of Bill's weight and his distance from fulcrum of seesaw as:

`50\text{ kg}\cdot x=60\text{ kg}\cdot 265\text{ cm}`

`\frac{50\text{ kg}\cdot x}{50\text{ kg}}=\frac{60\text{ kg}\cdot 265\text{ cm}}{50\text{ kg}}`

`x=\frac{6\cdot 265\text{ cm}}{5}`

`x=\frac{6\cdot 53\text{ cm}}{1}`

`x=318\text{ cm}`

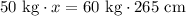
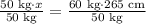
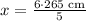
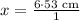
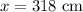
Therefore, Billy should be 318 cm far from the fulcrum to balance the seesaw.