Answer:
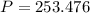 N
N
Block A will move first
Step-by-step explanation:
Let's call:
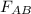 - the Force applied from A to B
- the Force applied from A to B
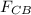 - the Force applied from C to B
- the Force applied from C to B
 - the Force applied by P
- the Force applied by P
Since the directions of all Forces above are towards B:
Angles between
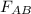 and
and
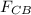 is
is
 °
°
Angles between
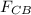 and
and
 is
is
 °
°
Angles between
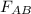 and
and
 is 180 - 85 - 20 = 75°
is 180 - 85 - 20 = 75°
From Sine's Law:
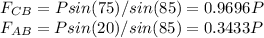
For Block A, from Newton's Law:
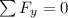 ⇒
⇒
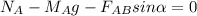
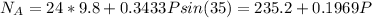
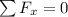 ⇒
⇒
 where
where
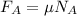
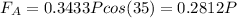
Since

Then
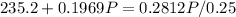 ⇒
⇒
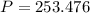 N
N
For Block B, from Newton's Law:
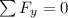 ⇒
⇒
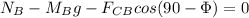
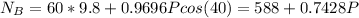
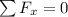 ⇒
⇒
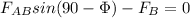 where
where

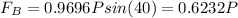
Since
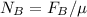
Then
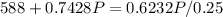 ⇒
⇒
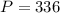 N
N
Hence,
Since the value of P is smaller for Block A than Block B, Block A will move first.
And the required value of P is smaller one among the above,
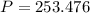 N
N