Question

Hi boys can you help me pls!!!!!!!

Rowan tosses a ball toward his opponent during a game of table tennis. Function h demonstrates the height of the ball, in meters, when it is a distance x meters away from Rowan.


h(x)=-1/4x^2+1/2x+1/2


Select the statement that accurately describes the maximum point of the graph modeling the height of the ball.


A.

The maximum height of the ball is 0.75 of a meter, which occurs when it is approximately 1 meter away from Rowan.

B.

The maximum height of the ball is 1 meter, which occurs when it is approximately 2.73 meters away from Rowan.

C.

The maximum height of the ball is 1 meter, which occurs when it is approximately 0.75 of a meter away from Rowan.

D.

The maximum height of the ball is 2.73 meters, which occurs when it is approximately 1 meter away from Rowan.

Answer 1

Answer: OPTION A.

Explanation:

Given the following function:

`h(x)=-(1)/(4)x^2+(1)/(2)x+(1)/(2)`

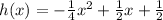
You know that it represents the the height of the ball (in meters) when it is a distance "x" meters away from Rowan.

Since it is a Quadratic function its graph is parabola.

So, the maximum point of the graph modeling the height of the ball is the Vertex of the parabola.

You can find the x-coordinate of the Vertex with this formula:

`x=(-b)/(2a)`

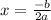
In this case:

`a=-(1)/(4)\\\\b=(1)/(2)`

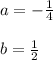
Then, substituting values, you get:

`x=(-(1)/(2))/((2)(-(1)/(4))))\\\\x=1`

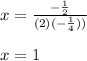
Finally, substitute the value of "x" into the function in order to get the y-coordinate of the Vertex:

`h(1)=y=-(1)/(4)(1)^2+(1)/(2)(1)+(1)/(2)\\\\y=0.75`

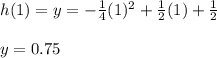
Therefore, you can conclude that:

The maximum height of the ball is 0.75 of a meter, which occurs when it is approximately 1 meter away from Rowan.